Non-Intuitive Topics

While a lot of things in electronics aren't particularly confusing, there's a few topics which I've found historically just a bit surprising and non-intuitive.

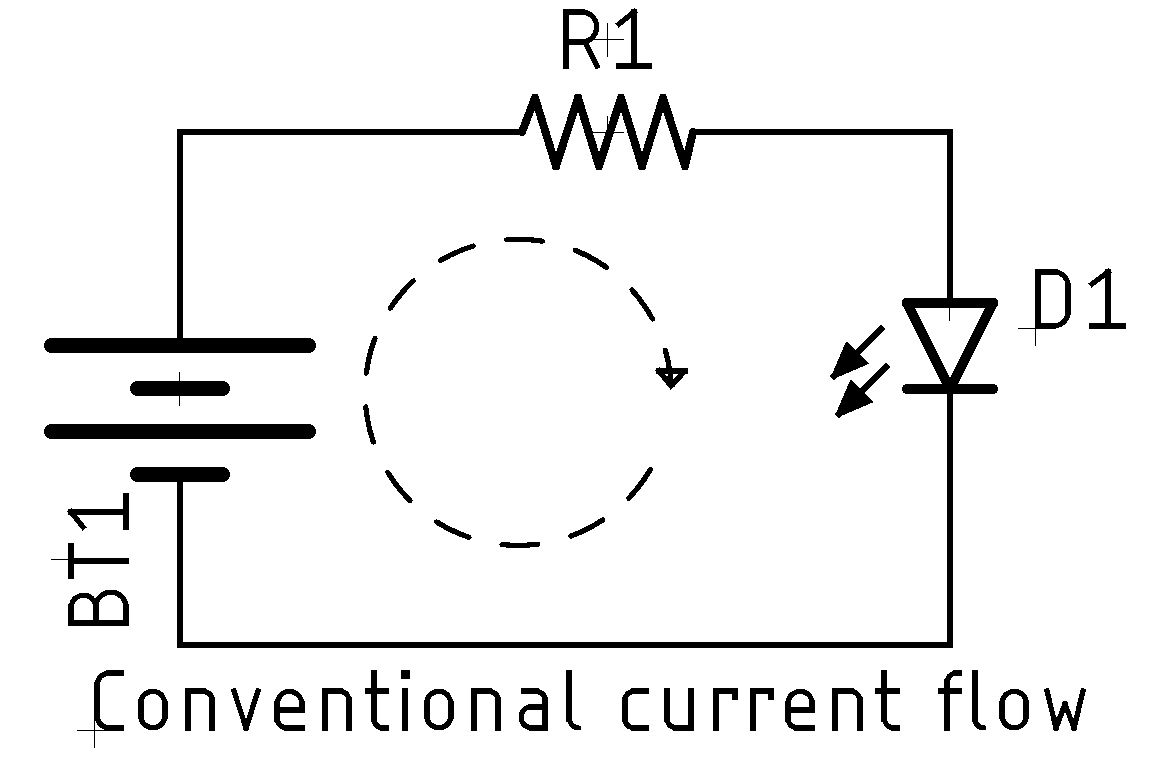
Conventional Current Flow v Reality

One thing that trips some people up---largely because you can ignore it until you can't---is the difference between reality and "classical" current flow. This confusion can all be laid at the feet of one man: Benjamin Franklin. When Franklin performed his famous kite experiment, thereby proving that lightning was electricity, the general concept of electricity was that it was some kind of "fluid". Franklin, understandably, surmised that the electrical flow proceeded from positive to negative. This idea was accepted, and it became the conventional view.

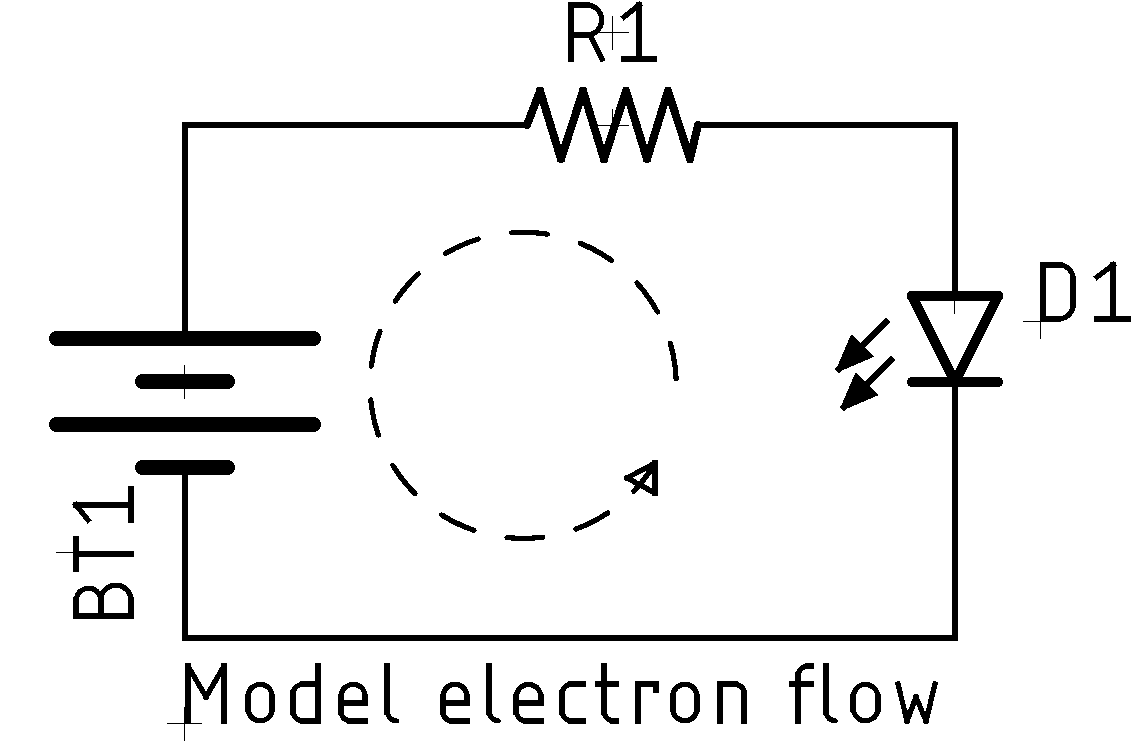
Today we call this the conventional current flow model, and in it, current flows from a more positive voltage to a less positive voltage. This all predates the modern (Rutherford, 1911) model of electrons, neutrons, and protons. Now we know that an electron is the charge carrier and that electrons travel in the reverse direction. Franklin was wrong. Electrons move from a lower potential to a higher potential. This is termed the model electron flow.

For most work, you can simply use the conventional flow and everything will be fine. It's probably easier to understand for most people. There are times, generally when thinking deeply about semiconductors, where electron flow is more easy to understand. If someone doesn't talk about what model they are using, 99.999% of the time they are using the historic conventional current flow model.

If you want to read more, this article might help.

Everything is a Sine wave

The sine wave is more than the simplest waveform we have, it's also, mathematically, the only wave form we have (ok, also cosines). Every other waveform is composed of some number of sine (and cosine) waves superimposed on one another (more on this later). First, let's start with the most basic of sine waves.

where:

• \(t\) is the time
• \(A\) is the amplitude, or peak deviation of the function from zero (not peak-to-peak)
• \(f\) is the frequency in oscillations per second
• \(\omega\) is the angular frequency (\(\omega = 2 \pi f\)) in radians per second.
• \(\varphi\) is the phase, specified in radians where in its cycle (think where on its curve) the sine wave is when \(t = 0\)

So far, so good, if you like trigonometry.

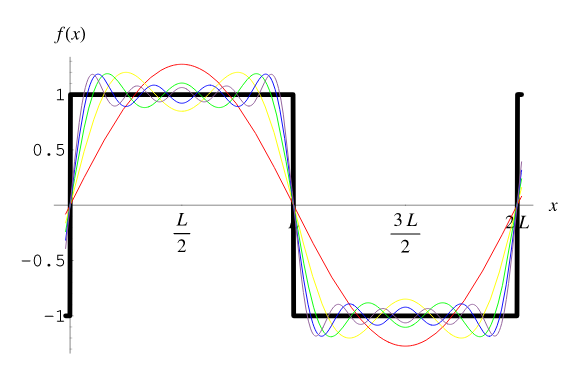
What Joseph Fourier proposed, quite radically, in the 19th century was that every waveform could be decomposed (or synthesized) by merging a large number of sine waves together. For example, a square wave, which seems at first glance to be the absolute opposite of a sine wave can be constructed using a Fourier series thusly:

Easy peasy, lemon squeezy, right?

Visually, this is more obvious:

Each of the colors represents another sine wave superimposed on the previous. As you can see with the fancy \(\infty\) in the equation, this is an infinite series. This is true of every waveform, just with different formulas and complexity.

When people talk about Fourier transforms (or sometimes FFT, fast Fourier transforms), what they are talking about is decomposing a waveform into its constituent sine waves (N.B. this is wildly oversimplified)

So how does this matter to us? Well, let's take a digital circuit running at 10MHz. Because digital circuits are mostly like a square wave (or at least attempt to behave that way), those 10MHz square waves are actually composed of an infinite number of sine waves at various harmonics of the fundamental square wave frequency. Some of those will have gigahertz frequencies.

Take, for example, a 1MHz square wave coming out of my signal generator and into my oscilloscope:

In it you can see the artifacts of the direct digital synthesis production of a square wave.

Even when you think you're not dealing with a high-frequency circuit, there actually is one underneath, just waiting to trip you up when you least expect it.

3rd Party Resources

• Square waves, or non-elephant biology